Paper Reading: VBase: Unifying Online Vector Similarity Search and Relational Queries via Relaxed Monotonicity

2024-02-17 约 5977 字预计阅读 12 分钟

VBase: Unifying Online Vector Similarity Search and Relational Queries via Relaxed Monotonicity

VBase: 通过 Relaxed Monotonicity (松弛单调性) 统一在线矢量相似性搜索和关系查询

Abstract

基于高维向量索引的近似相似度查询 approximate similarity queries已经成为许多关键在线服务的基础。对更复杂的向量查询的日益增长的需求要求将向量搜索系统与关系数据库集成在一起。然而，高维向量盘不表现单调性，而单调性是常规指标的一个重要性质。缺乏单调性迫使现有的向量系统依赖于 monotonicity-preserving tentative indices（为目标矢量的 TopK 近邻临时设置）来方便查询，由于难以预测最优 K，这将导致次优性能。本文介绍的 VBASE 系统能有效支持近似相似性搜索和关系运算符的复杂查询。VBASE 发现了一个共同属性 relaxed monotonicity 松弛单调性，从而将两个看似不兼容的系统统一起来。这一共同属性使 VBASE 能够规避仅 TopK 的限制，从而显著提高效率，同时证明它保留了基于 TopK 的语义。评估结果表明，在复杂的在线向量查询中，VBASE 的性能比最先进的向量系统高出三个数量级。VBASE 还能进行分析性相似性查询 analytical similarity queries，而以往的向量系统则无法做到这一点，而且在精确查询方面，VBASE 提高了 7000x speedup 的同时准确率达到 99.9%。

Introduction

深度学习（embedding）模型的最新进展是将几乎所有类型的数据（如图像、视频、文档）映射成高维向量。对高维向量的查询可以进行复杂的语义分析，这在以前即使不是不可能，也是很困难的，因此它们成为许多重要在线服务的基石，如搜索、电子商务和推荐系统。这些服务的 “在线” 性质要求矢量搜索以毫秒为单位完成。这种严格的延迟要求与精确搜索算法的固有高成本相冲突，迫使终端用户只能选择高维向量上的近似查询结果。随着新的矢量搜索应用不断涌现，矢量查询变得越来越复杂，通常涉及标量数据和矢量数据的混合搜索。这自然而然地推动了矢量搜索系统与关系数据库的整合。

矢量搜索和数据库系统使用索引的方式各不相同，而索引是加快查询速度的关键结构。传统索引（如 B-Tree）的一个重要特性是单调性。这一特性确保了查询可以在索引的引导下沿着某个方向单调地遍历数据集。这通常可以避免总数据扫描，从而提高查询执行效率。然而，由于维度诅咒（curse of dimensionality），对于高维向量索引来说，保持单调性的代价过于昂贵。取而代之的是，它们通常被组织成图或基于聚类的不规则结构，这种结构近似于单调性。遍历这样的向量索引并不能保证目标向量距离的严格单调性，但它能让系统有效地确定新的遍历何时不太可能到达比当前 K 个向量更接近目标的向量。因此，现代向量索引只支持近似 TopK，即近似查找 K 个近邻。TopK 查询会遍历向量索引足够多的步数，直到确定不可能找到比当前 K 个最近向量更近的邻居为止。

为了整合向量搜索和数据库系统，现有的向量数据库系统选择了严格的单调性。为了支持 TopK 以外的相似性查询，它们首先利用 TopK 收集 K 个向量，然后根据与目标向量的距离对 K 个向量进行排序，这样就建立了一个保持单调性的临时索引。因此，复杂的关系运算符可以按传统方式在临时索引上执行。考虑下面的向量搜索查询：“查找 X 个与图片最相似但低于某一价格的产品”。数据库规划者首先会在图像嵌入的向量属性上运行向量搜索运算符，以找到 K 个最近的图元，然后在价格属性上应用过滤运算符。但是，我们无法准确预测有多少图元会通过过滤运算符，这个数字可能远小于 K。因此，这种做法本身就难以确定能产生精确 X 结果的最佳 K。因此，它要么采用保守的大 K 设置，要么采用多个 K 的反复试验，这两种方法都会导致次优查询性能。

在本文中，我们介绍了 VBASE，这是一个新系统，能够高效地为复杂的在线查询提供服务，这些查询既涉及近似相似性搜索，也涉及标量和矢量数据集上的关系运算符。VBASE 将松弛单调性（Relaxed Monotonicity）作为从向量搜索系统和关系数据库这两个看似不同的系统中抽象出来的共同属性。松弛单调性要求索引遍历仅近似遵循单调性。我们观察到，最先进的矢量索引都以两阶段模式遵循松弛单调性属性：索引遍历首先近似定位离目标矢量最近的区域，然后以近似方式逐步远离目标区域。基于这一观察结果，我们正式定义了 “松弛单调性 “属性，它抽象了大多数现有矢量索引已经具备的核心索引遍历模式。松弛单调性可以看作是单调性的一种广义形式，因此也适用于传统的标量索引，如 B-Tree。因此，松弛单调性可以作为矢量搜索和数据库系统的共同基础

通过松弛单调性，VBASE 建立了一个统一的查询执行引擎，以支持对标量和矢量数据的各种查询，包括跨多个异构索引的查询 queries across multiple heterogeneous indices。VBASE 的统一引擎基于 Next 接口，而不是 TopK，以支持向量和标量索引的遍历。同时，该引擎允许从松弛单调性中推导出通用终止条件，以便及时停止查询的执行。

VBASE 的独特之处在于其基于松弛单调性的查询执行引擎可以证明其查询结果与最优 K 的 TopKonly 解决方案所产生的查询结果相当。这一强大的特性使 VBASE 能够规避 TopKonly 接口的限制，在保留基于 TopK 的查询语义的同时，显著提高效率。特别是，基于推导出的广义终止条件，VBASE 能够在索引遍历过程中检测 K，而无需预测 K。对于比 TopK 搜索更复杂的查询，VBASE 可以在结果准确性相似（即相同甚至更好的 recalls）的情况下，实现比最先进系统低达三个数量级的平均和尾部查询延迟。

此外，通过放松单调性，VBASE 甚至可以支持以往系统不支持的近似查询类型，并显示出卓越的查询性能和准确性。例如，VBASE 可以在 16 秒内完成 join-based vector query with 99.9%+ recall rate，比暴力表扫描快 7000 倍。

总之，本文做出了以下贡献：

VBASE 确定并正式定义了 “松弛单调性 Relaxed Monotonicity"，这一特性首次揭示了精心设计的向量指数的核心，以及它们在实践中有效工作的原因。
VBASE 基于松弛单调性构建了一个统一数据库引擎，可利用矢量和标量数据索引进行功能强大的复杂查询。
我们证明了 VBASE 的统一引擎使用向量索引产生的结果与纯 TopK 方法相当，其 execution plan 比纯 TopK 方法更有效。
我们在 PostgreSQL 的基础上实现了 VBASE，只增加了 2000 行代码，并展示了对混合 100 万配方数据集上的八个复杂 SQL 查询的端到端评估，这些数据集既有矢量属性，也有标量属性。我们计划将 VBASE 开源，以满足人工智能时代新出现的重要矢量分析应用。

Background

Emerging Online Vector Queries

在人工智能时代，矢量已成为一种重要的数据表示形式。深度学习已经促成了越来越多以向量为中心的在线应用，包括基于嵌入的检索、人脸识别、代码检索、问题解答、谷歌多重搜索、Facebook 近似重复检测等。最近，人工智能应用利用 ChatGPT 的检索插件，将其专有知识、个人文档和聊天上下文转换成向量。这样就能检索到有价格、类别、地点或时间限制的相关向量，从而在聊天中构建提示。

传统应用也受益于人工智能的向量。例如，搜索引擎将网络文档转化为词袋稀疏向量和深度学习填充密集向量，以提高搜索结果的相关性。而推荐系统则将图片、视频和商品描述转化为不同的向量。结合商品价格和类别等标量数据，这些向量可用于提升推荐体验。

所有这些都需要一个通用系统来高效运行复杂的矢量和标量查询。总之，这些向量应用场景可分为以下几类。 S1: 基于嵌入的检索、推荐和问题解答基本上都是在给定查询向量的情况下，在向量数据集中搜索 K 个最接近的向量。这类查询可以很自然地用单向量列上的 TopK 运算符来表达。 S2：单矢量 TopK 加标量属性过滤。在某些标量属性限制条件下，还需要找到 TopK 结果。Google Multisearch 就属于这一类。它允许用户在进行相似性图像搜索时提供额外的文本提示。 S3: 多列 TopK。有些矢量分析需要将不同矢量属性的多个 TopK 搜索结果进行交叉。例如，图像-食谱检索是一种对（矢量化）成分关键词和菜肴图像样本的多模态数据属性进行的食谱搜索。最近的研究表明，多列 TopK 搜索可以提高问题解答等应用的结果质量。 S4: 向量相似性过滤器。相似性过滤是典型的向量分析应用场景。例如，人脸识别和 Facebook 的近乎完全重复检测都是从具有相似性阈值的数据集中搜索相似图像（给定图像）。为了支持这类应用，我们可以使用基于两张图片之间距离相似性的矢量过滤，即基于距离的范围查询。所有这些矢量查询类型都有严格的延迟要求（如毫秒）。遗憾的是，现有系统都无法全面有效地支持所有这些在线相似性查询（见表 1）。

The Division Between Databases and Vector Search Systems

虽然数据库可以通过关系代数来表达上述查询，但由于向量索引和传统数据库索引在语义上存在分歧，因此很难提供一个统一的系统来高效运行各类复杂的在线向量查询，如表 1 所示。

关系数据库。关系数据库是运行复杂查询的最主要工具之一。为了满足低延迟的 “在线” 要求，数据库广泛采用索引来加速查询执行，如 B 树、B+ 树等。这些索引具有单调性（monotonicity），这种特性允许查询沿某个方向单调地遍历索引，例如，按降序或升序遍历。

在新兴向量场景中，最重要的在线查询类型之一是 TopK 查询。而传统的数据库索引可以通过按升序或降序遍历索引并在收集到 K 个结果后立即终止查询来加快 TopK 的速度。这种优化适用于许多 TopK 变体，如 TopK + 过滤和多列 TopK 查询。然而，这种优化的有效性依赖于单调性假设，而高维向量索引并不遵循单调性假设。接下来我们将详细说明。

Approximate vector search 近似向量搜索：最近，人工智能模型的爆发产生了大量且不断增长的高维向量数据。为了获得更好的学习表示，一个向量可以有数百个维度。由于维度诅咒，没有任何解决方案能在亚线性时间内完成高维向量查询。为了应对 “在线” 场景，现代向量搜索系统采用近似方法，在保持相对较高的结果准确率（90% 以上的召回率）的同时，大幅降低查询延迟（毫秒级）。这些系统通常被称为近似近邻搜索（approximate nearest neighbor search ANNS）系统。 与关系数据库一样，矢量索引也被用来促进近似矢量搜索。有代表性的矢量索引或以分区的形式组织（基于聚类、哈希、高维树，或以邻域图）。在高维空间中定位一个向量的难度迫使这些向量索引对近似 TopK 进行优化。在 TopK 查询中，索引遍历由查询向量 q 引导，根据 q 与某些锚点（如群集中心点或采样图顶点）之间的距离，近似地向最近的邻居迂回前进。在遍历过程中，q 的方向可能会发生巨大变化，因此该过程不能保证在每一步遍历中都接近 q，而且向量索引遍历也不是单调的。 矢量索引缺乏单调性使得数据库系统无法直接使用矢量索引来加速查询，这也是数据库和矢量搜索系统之间产生分歧的主要原因。

基于 TopK 的解决方案消除 division：由于矢量索引是为 TopK 优化的，ANNS 系统只提供一个 TopK 接口。为了缩小数据库和矢量搜索系统之间的单调性差距，目前的做法是使用 ANNS TopK 接口，根据与目标矢量的距离排序的 K 个矢量创建暂定索引。这种暂定索引能保持单调性，从而在数据库中实现快速矢量查询处理。

然而，基于 TopK 的暂定索引解决方案并不令人满意。要预测暂定索引 K 的正确大小是很困难的，甚至是不可能的，因为在查询中，带有过滤约束的后续关系运算符可以收集到正确数量的结果。这种限制普遍适用于 TopK + 过滤查询、向量相似性过滤查询等。因此，基于 TopK 的暂定索引不可避免地会导致保守地选择一个非常大的 K，或者对不同大小的 K 进行反复试验，这都会产生过多的数据访问和计算量。

VBASE Design

Relaxed Monotonicity

与传统标量索引不同，高维向量索引是为近似 TopK 而设计的，并不遵循单调性。图 1 显示了 FAISS IVVFlat 和 HNSW 这两种常用矢量索引的 TopK 遍历模式。如图所示，矢量指数遍历不符合单调性，随着遍历的进行，到目标矢量的距离会出现不可预测的波动。由于这些矢量索引缺乏单调性，关系数据库无法直接使用它们来加速查询。

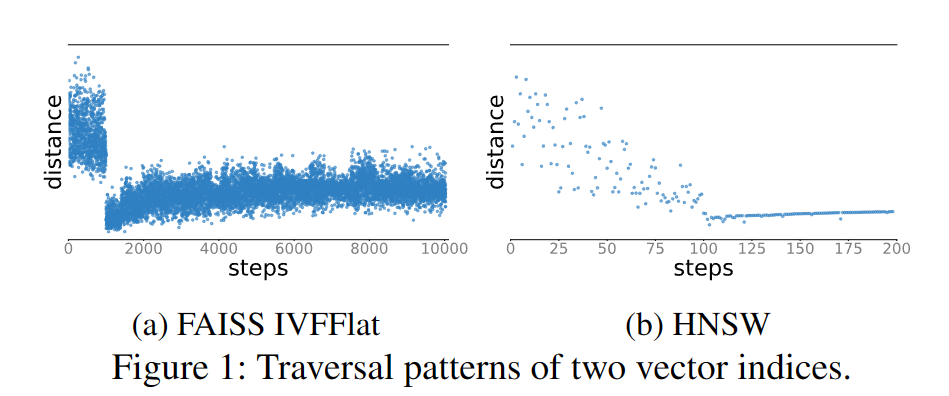
两阶段向量索引遍历模式：尽管如此，图 1 显示了两个矢量索引的两阶段索引遍历模式。在第一阶段，尽管矢量距离有较大波动，但索引遍历大致接近目标矢量区域。在第二阶段，指数遍历趋于稳定，并以近似方式稳步偏离目标矢量区域。这种两阶段遍历模式在我们研究的大多数向量指数中都很常见。我们认为，设计良好的矢量索引的本质是一种有效的数据结构，它隐含了这种遍历模式。因此，当 TopK 搜索查询进入第二阶段时，由于进一步遍历不可能识别出更多相似向量，因此可以提前终止。松弛单调性的正式定义。根据两阶段遍历模式，我们可以正式定义 “松弛单调性”（Relaxed Monotonicity），以确定向量索引遍历是否已进入第二阶段。该定义建立在向量 TopK 搜索内部执行方式的直观基础之上

图 2 展示了对查询向量 q 进行一般向量搜索的过程。图中虚线箭头表示与 q 相关的索引遍历路径。在高维空间中，q 的邻域由以 q 为中心的邻域球定义，如图 2 中的圆形所示。之后，索引遍历离开球体，进入第二阶段、在这一阶段，查询可以终止。图 2：松弛单调性直观示意图。向量查询 q 沿着遍历路径的前进方向发现了 q 与 E 个最近向量的邻域、

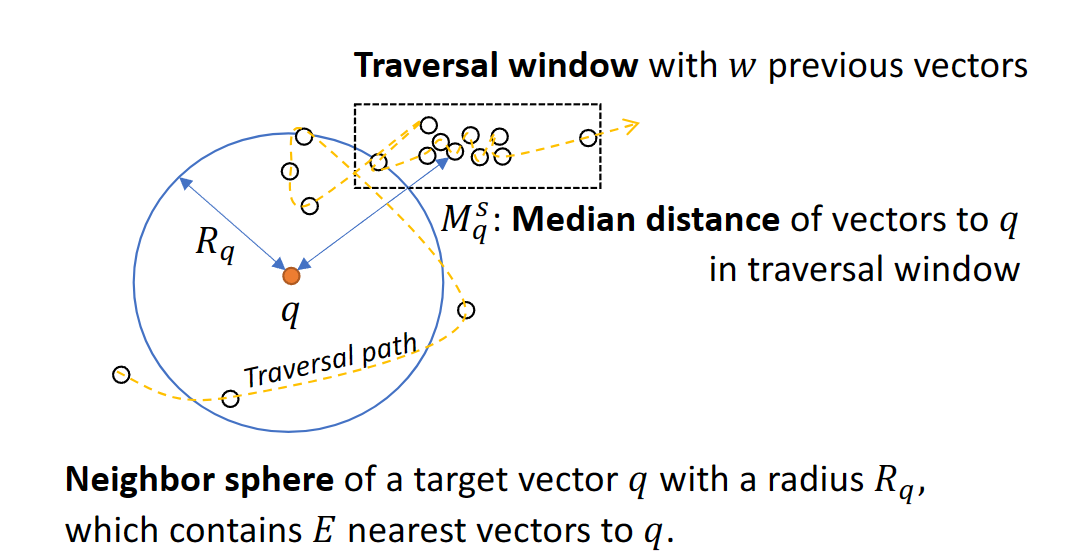
图 2 显示，要确定是否进入第二阶段，查询需要了解以 q 为中心的邻域球半径 Rq，以及查询的当前索引遍历位置（表示为遍历步长 s）与 q 之间的距离 Msq 是否大于 Rq，即是否超出了 q 的邻域。

形式上，Rq（q 邻域的半径）定义为：

Rq = Max(To pE({Distance(q,v j )|j ∈[1,s −1]})),

(1) 其中 To pE 表示遍历过程中观察到的 q 的 E 个最近邻，假设到目前为止遍历已经到达步骤 s。对于 K 个最近向量搜索查询，需要 E ≥K 才能产生足够的最终结果。在图 2 中，圆圈内的 E 向量是迄今为止访问的所有 s 个向量中 q 的最近邻。在索引遍历过程中，球体半径 Rq 在第 1 阶段会逐渐减小，并在第 2 阶段变得稳定。给定 Rq 的定义，系统需要定义 Msq，即目标向量 q 与当前索引遍历位置之间的距离测量，表示为遍历步长 s。然后使用 Msq 来判断遍历是否进入阶段 2，即离开邻居球体。数学上，Msq 被定义为最近 w 步中遍历的所有向量到 q 的中值距离，即遍历窗口。

Msq = Median({Distance(q,vi)|i ∈[s −w +1,s]}), (2) 其中 Distance(q,vi) 表示 q 与向量 vi 之间的距离，在过去的遍历中窗户。请注意，我们使用中位数而不是均值来忽略遍历窗口中的任何离群向量，这些向量与 q 的距离比其他向量过大或过小。例如图 2 所示遍历窗口中最左边和最右边位置的两个离群值向量。

看不懂

Summarization: The paper identifies a common property, relaxed monotonicity, to unify two seemingly incompatible systems: vector search systems and relational databases, and proposes VBase that can handle complex queries of both approximate similarity search and relational operators on high-dimensional vector data. Relaxed monotonicity allows VBase to circumvent the constraints of a TopK-only interface and achieve significantly higher efficiency, while provably preserving the semantics of TopK-based solutions. The paper also presents a PostgreSQL-based implementation of VBase and compares it with other open source systems.

Contribution: The paper introduces the concept of relaxed monotonicity, a property that can unify vector similarity search and relational queries, and leverages it to perform early termination of vector search.

VBase builds a unified database engine based on relaxed monotonicity and modifies the original topk vector query interface so that the vector index can continuously spit out results to downstream operators, it can be easily connected to the volcano model of traditional relational databases. VBase has the same accuracy as the pure TopK method, and the execution plan is more efficient

The paper implements VBASE based on PostgreSQL, adding only 2,000 additional lines of code, and compares it with other open source systems. It shows that VBase achieves up to three orders-of-magnitude higher performance than state-of-the-art vector systems on complex online vector queries.

Limitation

Key concepts and algorithms lack relatively clear definitions and descriptions, and there may be some confusion. It does not provide a clear and formal definition of relaxed monotonicity, the cost estimation and query planning methods.

The paper does not discuss the limitations and assumptions of the relaxed monotonicity property. For example, how does it cope with dynamic and evolving data and queries?

Improve: Run a series of hybrid queries on VBase and AnalyticDB-V systems, and measure their performance and accuracy using various metrics. Analyze the results and identify the strengths and weaknesses of both systems since they both combine vector similarity search and relational queries. Provide more rigorous and formal definitions and proofs of the relaxed monotonicity, the cost estimation and query planning methods, and discuss their limitations and assumptions to help to clarify and validate the core concept of the paper.

目录