Paper Reading: The Case for a Learned Sorting Algorithm [SIGMOD 2020]

The Case for a Learned Sorting Algorithm

除了 Query Optimization, Index, Tunning, ML 还可以用在 Database 其他方面，比如排序？

论文作者中的 Tim Kraska 以及其团队，是 SageDB, Bao: Learned Query Optimization, Neo 的作者，此外还有 FITing-Tree 索引结构。

看了一下 Tim 除了在 MIT 当 AP，还在一家叫 Einblick 的公司创业（看了下好像是 text2SQL 类型的，应该已经被 Databricks 收购了），然后在 Amazon 研究 Data Science 和 AI 的结合？最近也有一些比如 2023 的 BRAD: simplifying cloud data processing with learned automated data meshes 和之前看的 SEED: Domain-specific data curation with large language models 也是 Tim 团队的，他们做了很多 AI 与数据库、数据、数据结构、数据处理结合的事情。

回到本篇，ML 排序和 Query Optimization 的思路差不多，比较重要的一点都是需要 ML 学习数据的分布函数：cumulative distribution function (CDF)，也是 SageDB 当中重要的一点。

ABSTRACT

Sorting is one of the most fundamental algorithms in Computer Science and a common operation in databases not just for sorting query results but also as part of joins (i.e., sort merge-join) or indexing. In this work, we introduce a new type of distribution sort that leverages a learned model of the empirical CDF of the data. Our algorithm uses a model to efficiently get an approximation of the scaled empirical CDF for each record key and map it to the corresponding position in the output array. We then apply a deterministic sorting algorithm that works well on nearly-sorted arrays (e.g., Insertion Sort) to establish a totally sorted order.

leverages a learned model of the empirical CDF of the data

看上去是先映射/分区，然后用插入排序在几乎有序的数组上排序，速度应该是很快的。和 C++ STL sort 思想也差不多，近乎有序就直接插入排序（当快速排序递归子区间足够小的时候，插入排序）

We compared this algorithm against common sorting approaches and measured its performance for up to 1 billion normally-distributed double-precision keys. The results show that our approach yields an average 3.38× performance improvement over C++ STL sort, which is an optimized Quicksort hybrid, 1.49× improvement over sequential Radix Sort, and 5.54× improvement over a C++ implementation of Timsort, which is the default sorting function for Java and Python.

实际上 C++ STL sort 又叫 Introsort，也就是 Hybrid Quicksort，没有稳定性。而 TimSort 是保持稳定性的归并和插入混合排序。

前两年出现了一个更快的 pdqsort，Rust 和 Go 也将其引入了标准库。主要思想也是拆分成几种情况，正常 quicksort，短的近似有序的用 insertion sort 最坏情况用 heapsort 保证最坏 nlogn 时间复杂度。但明显 pdqsort 也是不稳定的。

radix sort 就是基数排序，按照数位从低到高 / 从高到低排序。不仅整数也支持浮点数。

INTRODUCTION

对比了 radix sort （按 key 排序）和比较排序，提出用 Tim 团队在 SageDB 中的一个想法： ML 增强排序算法。

核心思想：we train a CDF model $F$ over a small sample of keys $A$ and then use the model to predict the position of each key in the sorted output. If we would be able to train the perfect model of the empirical CDF, we could use the predicted probability $P$ ($A ≤ x$) for a key x, scaled to the number of keys $N$, to predict the final position for every key in the sorted output: $pos = FA(x) · N =P (A ≤ x ) · N$ . Assuming the model already exists, this would allow us to sort the data with only one pass over the input, in $O(N)$ time

还是一个强前提，必须训练一个完美的 CDF model，先不说训练时间，训练精度能否拟合都是个问题

Obviously, several challenges exists with this approach. Most importantly, it is unlikely that we can build a perfect empirical model. Furthermore, state-of-the-art approaches to model the CDF, in particular NN, would be overly expensive to train and execute. More surprising though, even with a perfect model the sorting time might be slower than a highly optimized Radix Sort algorithm. Radix Sort can be implemented to only use sequential writes, whereas a naïve ML-enhanced sorting algorithm as the one we outlined in [28] creates a lot of random writes to place the data directly into its sorted order

自己也提出了问题：perfect empirical model 完美的经验模型是不存在的。训练方法 NN 也比较昂贵？而且就算完美的 CDF 模型，也可能比 radix sort 慢。但不太懂什么是 highly optimized radix sort，是只有顺序写的吗？而 ML sort 可能会产生许多随机写入，导致有很多 IO 代价？不知道是不是 SageDB 遇到的问题。

本文提出了 Learned Sort，sequential ML-enhanced sorting algorithm 来解决这些问题。此外还有 a fast training and inference algorithm for CDF modeling.

本文应该是第一篇 cache-efficient ML-enhanced sorting algorithm which does not suffer from the random access problem.

1. We propose a first ML-enhanced sorting algorithm, called Learned Sort, which leverages simple ML models to model the empirical CDF to significantly speed-up a new variant of Radix Sort
2. We theoretically analyze our sorting algorithm
3. We exhaustively evaluate Learned Sort over various synthetic and real-world datasets

LEARNING TO SORT NUMBERS

pdf: 概率密度函数，连续随机变量。CDF: 累积分布函数，分布函数，概率密度函数的积分，能描述一个随机变量 x 的概率分布。

高斯分布的概率密度函数很常见，它的累积分布函数，取积分后就是 0 到 1 很像 sin 函数，是严格递增的

通过 CDF 能知道一个数据大概在什么区间的概率，乘上长度就可以知道位置，最后数组就是接近有序的

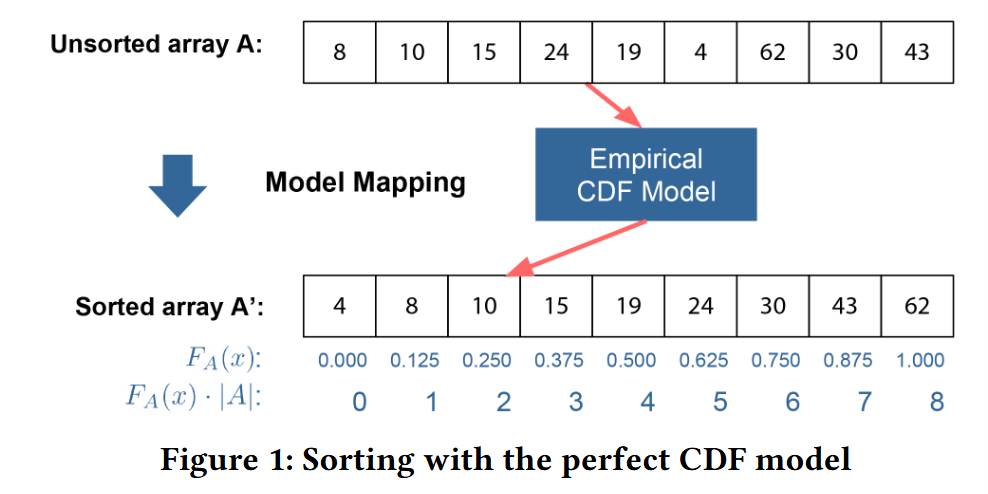
Given a function FA(x), which returns the exact empirical CDF value for each key x ∈ A, we can sort A by calculating the position of each key within the sorted order as pos ← FA(x )· |A|. This would allow us to sort a dataset with a single pass over the data as visualized in Figure 1

但不可能会有完美的 CDF 函数，而且也只能选取数据中的一些样本来训练模型，而且数据会有重复。

讨论了 out-of-place 和 in-place 两种？

看上去还需要额外的辅助空间

Sorting with imprecise models

duplicate keys and imprecise models may lead to the mapping of multiple keys to the same output position in the sorted array.

Moreover, some models (e.g., NN or even the Recursive Model Index (RMI) [29]) may not be able to guarantee monotonicity, creating small misplacements in the output. That is, for two keys a and b with $a < b$ the CDF value of a might be greater than the one of $b (F (a) >F (b))$, thus, causing the output to not be entirely sorted.

如何解决重复键、不精确模型的问题？

此外模型还可能不是单调的

所以如果位置发生碰撞 collisions，和哈希方法一样采用了 Linear probing, Chaining, Spill bucket 等方法来解决冲突。

Linear Probing 会导致错的键越来越多，尤其是非单调的时候。其他方法会增加空间开销，比如 spill bucket 用新的桶存，则需要单独归并。

论文都采用了 spill bucket 的方法，对于非单调的情况，用插入排序来解决问题。

the expected number of collisions depends on how well the model overfits to the observed data.

说了一堆，就是碰撞的概率还是很高，除非是完美的 CDF，但是有需要减少训练时间，而且只能抽取样本训练，没法学到完美的 CDF

使用了额外的辅助空间解决 collision。

就算完美 CDF 也比 Radix 慢，但是为什么呢？

这一部分分析说认为是随机访问导致了 CPU cache 和 TLB 局部性失效，而 radix 是顺序写入的，能够利用缓存和局部性。所以本文还提出了利用缓存的 ML-enhanced 算法

Cache-optimized learned sorting

其实 ML sort 和 Radix 很像，都是 bitmap 类型的，论文也提到如果 the number of elements to sort is close to the key domain size (e.g., 23^2 for 32-bit keys) 就是几乎一致的。

所以主要是和 radix 比较？

radix 速度取决于 key domain size，而当元素数量远小于 key domain size 时，Learned Sort 速度也比 radix 快很多。

1. We organize the input array into logical buckets. That is, instead of predicting an exact position, the model only has to predict a bucket index for each element, which reduces the number of collisions as explained earlier.
2. Step 1: For cache efficiency, we start with a few large buckets and recursively split them into smaller ones. By carefully choosing the fan-out ( f ) per iteration, we can ensure that at least one cache-line per bucket fits into the cache, hence transforming the memory access pattern into a more sequential one. This recursion repeats until the buckets become as small as a preset threshold t . Section 3.1 explains how f and t should be set based on the CPU cache size.
3. Step 2: When the buckets reach capacity t , we use the CDF model to predict the exact position for each element within the bucket.
4. Step 3: Afterwards we take the now sorted buckets and merge them into one sorted array. If we use a non-monotonic model, we also correct any sorting mistakes using Insertion Sort.
5. Step 4: The buckets are of fixed capacity, which minimizes the cost of dynamic memory allocation. However, if a bucket becomes full, the additional keys are placed into a separate spill bucket array (see Figure 4 the “S”bucket symbol). As a last step, the spill bucket has to be sorted and merged. The overhead of this operation is low as long as the model is capable of evenly distributing the keys to buckets.

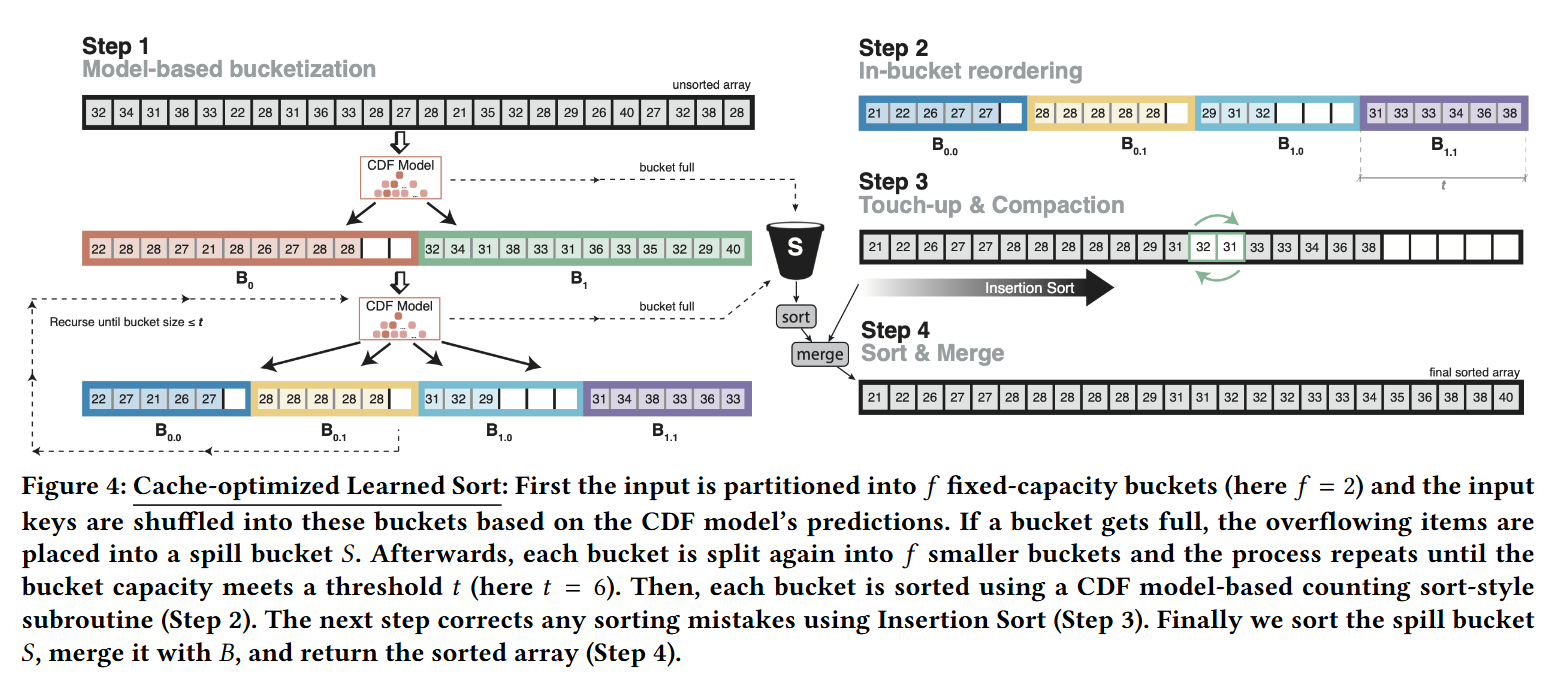
cache-optimized learned sort 有几个优化：1. 预测桶的位置，避免碰撞 2. 为了提高缓存效率，采用几个大的桶，分成小的桶，选择一个 fan-out f 函数？ 3. 桶达到容量时，用 CDF 模型预测位置 4. 如果用非单调模型，用插入排序修正 5. 小桶容量固定，还有溢出 spill bucket

还是要保证 CDF 的拟合程度，以及分布的均匀性

算法细节略

Implementation optimizations

实现上有几个优化

1. We process elements in batches. First we use the model to get the predicted indices for all the elements in the batch, and then place them into the predicted buckets. This batch-oriented approach maintains cache locality
2. As in Algorithm 1, we can over-provision array B by a small factor (e.g., 1.1×) in order to increase the bucket sizes and consequently reduce the number of overflowing elements in the spill bucket S. This in turn reduces the sorting time for S.
3. Since the bucket sizes in Stage 2 are small (i.e., b ≤ t ), we can cache the predicted position for every element in the current bucket in Line 28 and reuse them in Line 34.
4. In order to preserve the cache’s and TLB’s temporal locality, we use a bucket-at-a-time approach, where we perform all the operations in Lines 11-40 for all the keys in a single bucket before moving on to the next one. The code for the algorithm can be found at http://dsg.csail.mit.edu/mlforsystems.

首先这是批处理的，先预测位置，然后入桶，能够保证缓存局部性。可以增加辅助数组的大小？减少桶溢出的概率。而且桶大小很小，可以重复利用。最主要的是 bucket-at-a-time approach，每次只处理一个桶里的所有键，提高缓存局部性。

算法 2 比较长，但大致思路就是利用小桶（桶和桶之间应该也是有序的）局部性，而且能够避免部分碰撞

只是这个桶的数量要怎么选呢？论文好像没有仔细讲。而且关于稳定性，只是稍微讲了一句只要溢出桶的排序是稳定的，则 Learned Sort 是稳定的，我觉得可以多讨论一下和验证，尤其是当溢出桶数据比较多的时候，选择什么算法？是插排还是归并？还是需要分析算法的。

Choice of the CDF model

如何选取 CDF model？虽然论文说不取决于特定的模型，但是还是需要考虑训练和推理快的。

Thus, models such as KDE[43, 47], neural networks or even perfect order-preserving hash functions are usually too expensive to train or execute for our purposes. One might think that histograms would be an interesting alternative, and indeed histogram-based sorting algorithms have been proposed in the past. Unfortunately, histograms have the problem that they are either too coarse-grained, making any prediction very inaccurate, or too fine-grained, which increase the time to navigate the histogram itself (see also Section 6.8).

Certainly many model architectures could be used, however, for this paper we use the recursive model index (RMI) architecture as proposed in [29] (shown in Figure 5). RMIs contain simple linear models which are organized into a layered structure, acting like a mixture of experts[29].

考虑了一些传统的 NN 或者带顺序的哈希，甚至直方图，但可能不太准或者粒度太细。

还是使用了 SageDB 中提出的 recursive model index RMI 模型，

推理速度很快，一次加法、乘法和查找

训练：采样几个输入，然后排序之后(std::sort), 生成了一棵树，自顶向下训练一个线性模型。除了三维也可以二维，

单个模型的训练，为了保证模型是单调的，算法 2 就不需要插入排序修正，需要训练时进行边界检查，但又会使得算法 2 需要额外的分支命令（没有 cache？）

用了单调性更好的 linear spline fitting？训练快，插入排序也减少了 35% 的 swap

ALGORITHM ANALYSIS

讨论时间复杂度和性能，以及不同参数下的表现

Analysis of the sorting parameters

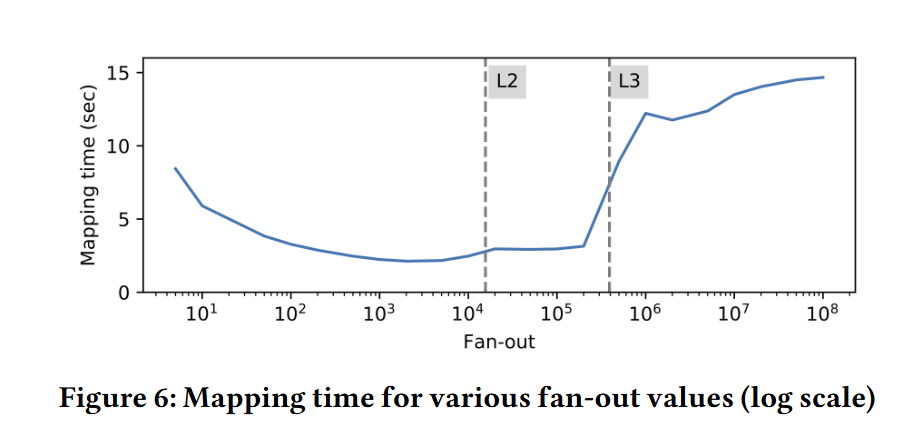
3.1.1 Choosing the fan-out ( f )

f 大，可以使得模型更准？那不就成了 radix 吗

为了利用缓存，f 也必须要限制。测试了 100m doubles 和不同的 f，表现了其性能和 L1 L2 cache size(f = 1-5K) 相关。

3.1.2 Choosing the threshold ( t ). The threshold t determines the minimum bucket capacity as well as when to switch to a Counting Sort subroutine (Line 11 in Algorithm 2). We do this for two reasons: (1) to reduce the number of overflows (i.e., the number of elements in the spill bucket) and (2) to take better advantage of the model for the in-bucket sorting. Here we show how the threshold t affects the size of the spill bucket, which directly influences the performance

t 是 bucket size，会影响溢出的概率

论文也提到，基于样本训练，不可能会有完美的模型，不可能可以把每个元素映射到唯一的位置，总是会发生不同元素映射到同一个位置。这里推导了 E[s] = N / e 表示溢出桶的大小，N 表示桶的数量，论文通过测试不同的大小，当 t = 100 时，overflow 概率 3.9% < 5%, Learned Sort 性能最好。但说的是经验上来看？没有给出合理的证明和更详细的测试。

3.1.3 The effect of model quality on the spill bucket size.

不同模型会导致碰撞、溢出。论文假设样本是从分布中独立生成的？这部分没看懂，对于小样本，怎么学习分布才能导致溢出更少？反正还是要尽可能地拟合 CDF

3.1.4 Choosing the sample size.

太多经验操作了，直接就 1% 采样率了，而且他这个采样率只测试了采样率和训练/排序的时间，没有测其他参数？

Complexity

This process takes $O(N ·L)$ time, where L is the number of layers in the model. Since we split the buckets progressively using a fan-out factor f until a threshold size t , the number of iterations and the actual complexity depend on the choice of f and t . However, in practice we use a large fan-out factor, therefore the number of iterations can be considered constant

t 和 f 之间是否存在关系？时间复杂度 O(N L) L 是模型层数？f 比较大，迭代次数是常数级别的？

最重要的问题还是取决于模型质量，不论是什么阶段，如果模型太差，基本就是退化到插入排序，O(n^2)，桶的溢出也受影响，溢出桶也受影响。

算法使用了辅助空间，空间复杂度 O(N) 但后续实现了 in-place 的 O(1) 空间复杂度

EXTENSIONS

在字符串上 in-place 排序

Making Learned Sort in-place

还是分组，但是是用 buffer

Learning to sort strings

字符串和浮点数的区别

但是怎么训练 CDF？限制字符有可能导致非单调。

Duplicates

重复值产生很大影响，会导致很多碰撞。

比如 [0,1,0,1,0,1] 这种数据，应该会导致很多问题

RELATED WORK

排序算法通常被分类为 基于比较 或 基于分布 的

Comparison sorts:

Distribution sorts:

SIMD optimization

Hashing functions

ML-enhanced algorithms

神奇的是，这一部分提到了 Swift5 换了新的 PDQSort，论文却没有进行对比？

论文还提到了 radix 非常适合 SIMD 和多核场景，不知道 Learned Sort 能否也扩展到这种情况

CDF model 和 order-preserving 哈希函数很像，但 CDF 还是需要分类，而 hash 训练慢而且一般没有 order-preserving

EVALUATION

• Evaluate the performance of Learned Sort compared to other highly-tuned sorting algorithms over real and synthetic datasets • Explain the time-breakdown of the different stages of Learned Sort • Evaluate the main weakness of Learned Sort: duplicates • Show the relative performance of the in-place versus the out-of-place Learned Sort • Evaluate the Learned Sort performance over strings.

6.1 Setup and datasets

这里还是比较了 PDQ 的，但是认为 PDQS 比 baseline 差很多？这不太合理吧。。PDQS 能消除很多分支预测，时间复杂度应该也是 O(nk) 和 O(nlogn) 级别的

而且训练时间也算入了排序时间，除非另有说明

synthetic datasets: 不同分布的，混合分布的，

真实数据：地图数据、物联网数据、FaceBook Rw 数据、TPC-H（其实也不是真实的）

对比的数据是 Sorting Rate，吞吐量，Learned Sort 都比较高，而 IS4o 和 Radix 比较接近，其他都没有太高

我认为他这个测试对传统的排序算法不是很好，传统的排序吞吐量都比较低。而且不太理解这个指标的概念是什么，不直观

Overall Performance

Sorting rate

没能看到 runtime, memory usage, comparisons/swaps 等更多指标

Sorting Strings

这里就排除了训练时间，而且去掉了 Radix，比 baseline 慢很多

Learn sort 在这里的吞吐量并不是很高，几乎是浮点数的十分之一，但还是要比 IS4O 高，比传统排序也高

The impact of duplicates

这里很有意思，重复很多的时候，Learned Sort 吞吐量变化其实并不大？只有非常多重复的时候才会降低很多。

In-place sorting

吞吐量下降了 10% 左右

Performance decomposition

大部分时间在桶分类

Using histograms as CDF models

RMI 模型更适合，更快，用了连续函数

CONCLUSION AND FUTURE WORK

加速分类，对字符串处理和排序做了展望，以及并行、多核排序、SIMD 等等。还有更多复杂类型

是一篇很好的论文，但 evaluation 只有一个指标，不知道能不能优化一下 std::sort 之类的 cache，不知道表现会怎么样。

The paper proposes a sorting algorithm called Learned Sort, which is developed from learned database SageDB by the same team. Learned Sort leverages machine learning (ML) to predict the sorted position of elements, significantly improving sorting efficiency for large datasets. The main idea is to train a CDF model over a small sample of the data and then use the model to predict the position of each key. In addition, the paper also proposes a highly optimized Learned Sort algorithm to maximize cache utilization with bucketization, and compares its performance between in-place and out-of-place implementation. Learned Sort outperforms existing sorting algorithms, particularly when dealing with large datasets that overflow the CPU’s cache. The paper also discusses where Learned Sort can be improved, such as more complex data types and parallel multicore sorting.

Contributions:

1. The paper propose the first ML-enhanced sorting algorithm, Learned Sort, which leverages RMI to model the empirical cumulative distribution function (CDF) of the data. The prediction allows Learned Sort to directly place elements close to their final position, reducing the number of comparisons and swaps needed compared to traditional comparison-based sorting methods.
2. Besides the basic ML-enhanced sorting algorithm, the paper also explores an optimized Learned Sort algorithm that can take advantage of caching, and provides an exhaustive comparison with Radix Sort with large datasets. Optimized Learned Sort makes use of buckets and spill buckets for sorting, and the paper also presents an improved version that does not require auxiliary space that can sort in-place.
3. The paper provides a detailed theoretical analysis of Learned Sort, and also gives complete evaluations based on the analysis, comparing not only traditional sorting algorithms such as std::sort and Timsort, but also the optimized Radix Sort and IS4o. The experimental result proves that Learned Sort has better throughput with large datasets (real-world, synthetic, mixed distributions, and large number of duplicates).

Limitations:

1. Learned Sort heavily relies on the CDF models to predict the positions of keys. Not only it relies on the accuracy of the model, the paper also points out that even if there is a perfect prediction model, collisions will inevitably occur due to the sampling method used in training.
2. There are too few metrics for evaluation, the paper only compares sorting rate, which may not show the performance of Learned Sort in other aspects, such as runtime, memory usage, exchange rate or comparison ratio, etc. Compared with floating numbers, the throughput of Learned Sort drops sharply, which means that it is necessary to compare other metrics.
3. The paper’s comparison of Recursive Model Index (RMI) and other CDF models is less detailed, especially how to select the fan-out function f and bucket size t under different models, and the impact on overflow and spill buckets. In addition, the paper does not discuss the internal relationship between f and t. And when analyzing the algorithm, the paper doesnot give detailed proof that the algorithm is stable or unstable.

Improve:

First I would try to explore some techniques like transfer learning to leverage a pre-trained model on a broader data set like Zero-shot model, which could improve Learned Sort’s performance on new data types without retraining. And according to different CDF models, I will try to select different parameters such as fan-out function f and bucket size, discuss the relationship between them. Then I would try to optimize std::sort and timesort and even pdq sort to make them take advantages of cache and sequential writes, making a more detailed evaluation based on various metrics, such as runtime and memory usage. This paper is very innovative and well written, and I might also try some parallel processing techniques like SIMD, which can significantly speed up the sorting algorithm.